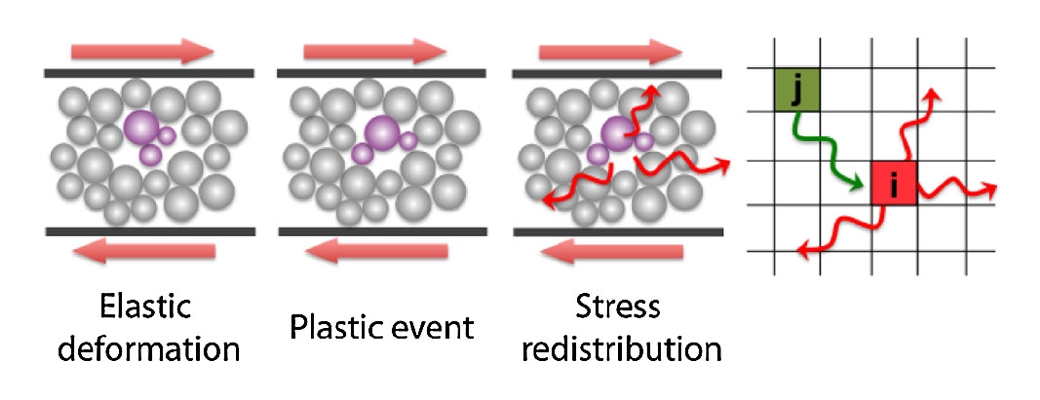
A common general idea is that the deformation in glassy systems will take place in
'weak' zones, somehow characterized by abnormally low elastic constants and increased
mobility. Here we test on atomistic numerical simulations the potential of the local elastic constants to predict failure in a model sheared glassy material.
One of the great scientific challenges is to find a new paradigm for the deformation and flow of disordered and glassy materials in the spirit of what was initiated by Peierls, Nabarro, Friedel in the 50’s and now well understood for defects and dislocations in cristals.
We have developed new methods to bridge the gap between the atomic scale description and the continuum description of matter.
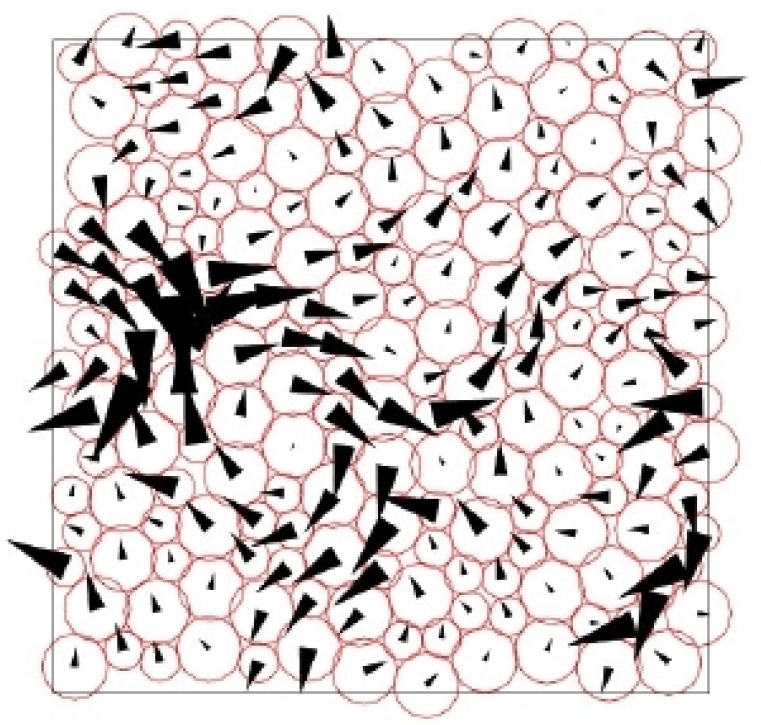
The phenomenon of strain localization in disordered systems is ubiquitous in nature and remains largely unexplained.
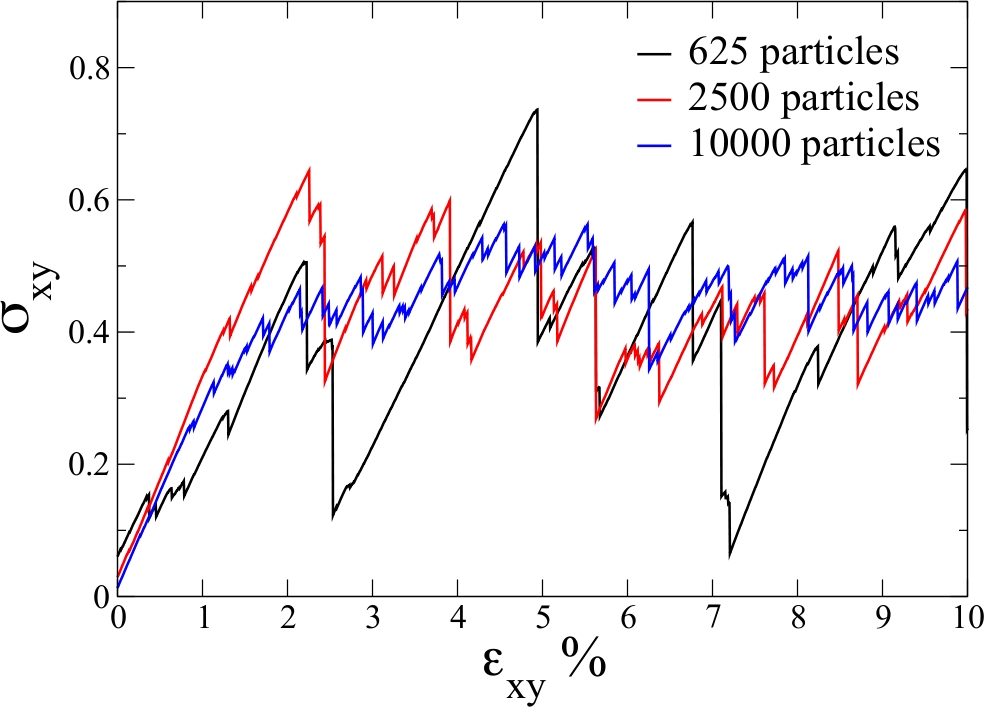
When subjected to slow driving many systems exhibit an intermittent response with the appearance of discrete and impulsive events spanning a broad range of sizes. Such a scale-invariant behavior is generally the signature of a heterogeneous underlying deformation.
The microscopic approaches are invaluable to identify the elementary relaxation processes in glassy or disordered materials and their interactions.
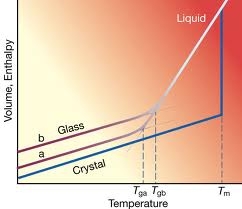
Glass formation
Scientists are still puzzled by what is sometimes referred to naively as a fourth state of matter, in addition to solid, liquid and gas.
Many phenomenological models of the rheology of glassy materials developed in recent years are located at an intermediate mesoscopic scale.
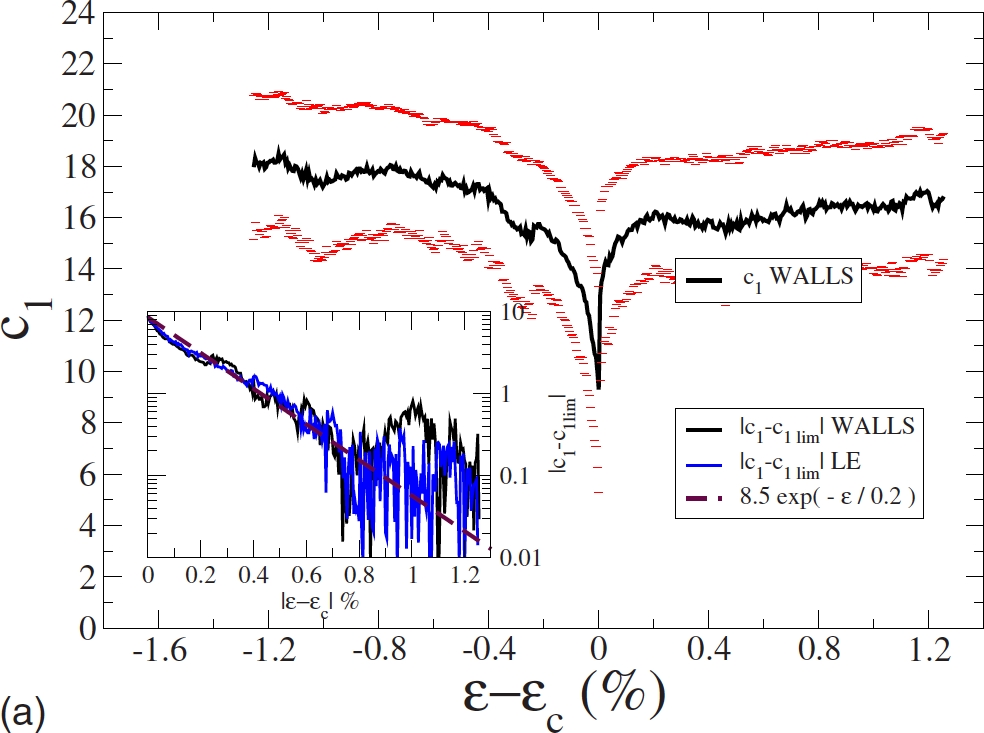
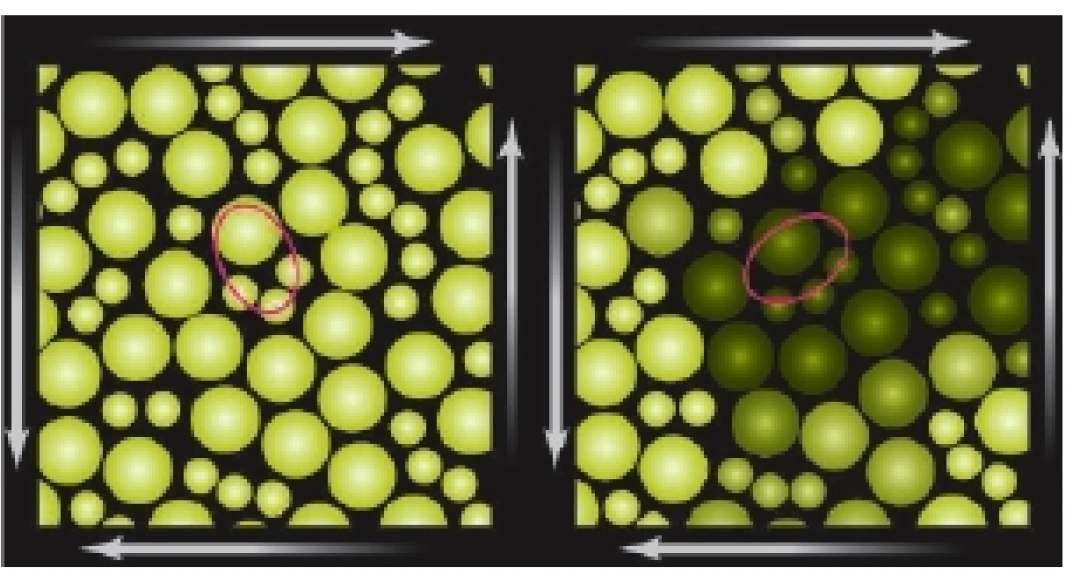
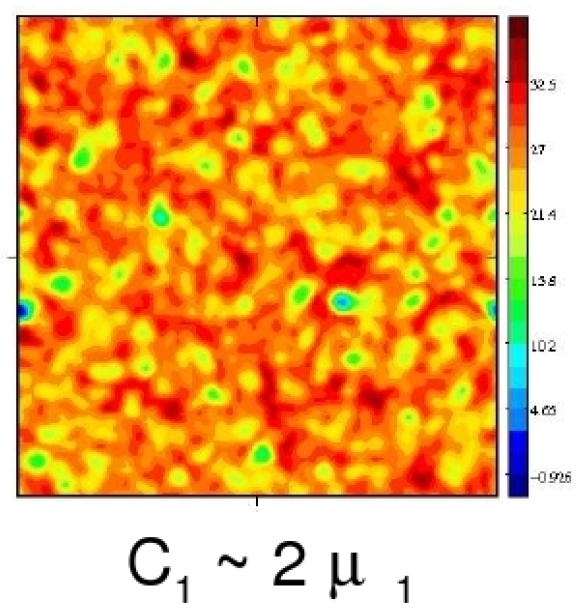
We calculate the local elastic moduli in a model glass system undergoing a quasistatic shear deformation at zero temperature and show that the glass appears as a
composite material composed of a rigid scaffolding and of soft zones.